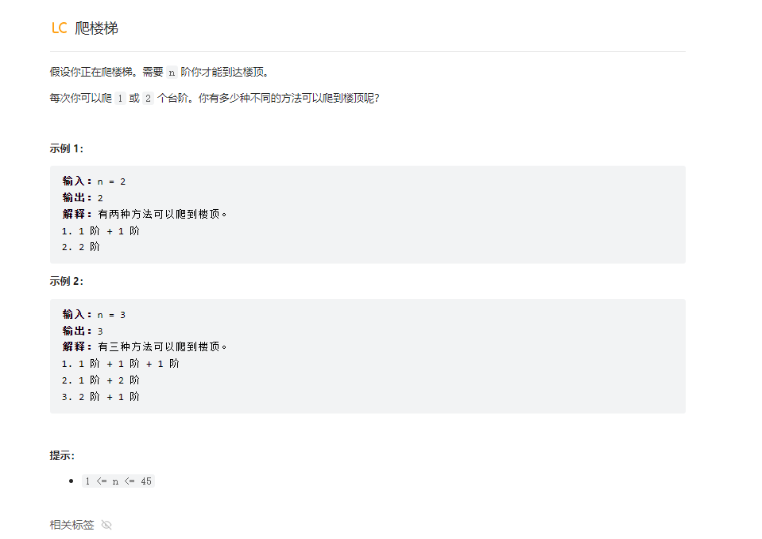
原题出处：https://leetcode.cn/leetbook/read/top-interview-questions-easy/xn854d/

解法一：

class Solution {
    public int climbStairs(int n) {
        return climbStairs(n,1,1);
    }

    public int climbStairs(int n,int a,int b) {
        if (n<=1) {
            return b;
        }
        return climbStairs(n-1,b,a+b);
    }
}

思路：尾递归，f(n)=f(n-1)+f(n-2)，从第三步开始，之后的每一步都是前两步之和。

解法二：

class Solution {
    public int climbStairs(int n) {
        if (n <=2) {
            return n;
        }
        int first = 1,second = 2,sum = 0;
        while (n-- > 2) {
            sum = first + second;
            first = second;
            second = sum;
        }
        return sum;
    }

}

思路：非递归的方式，我们知道除第一个方法总数和第二个方法总数，它的之后每一个方法的总数都为前两个方法总数的和。循环遍历计算每一步方法的总数，然后相加即可得到结果。

解法三：

class Solution {
    public int climbStairs(int n) {
        if (n == 1 || n== 2) {
            return n;
        }
        return climbStairs(n-1)+climbStairs(n-2);
    }

}

思路：递归的方式，但是这种方法递归的层次会比较深，会出现超时的问题，所以推进使用第一种尾递归的方式。

2025-06-10 start:

解法四（java）：

class Solution {
    public int climbStairs(int n) {
        if (n < 3) {
            return n;
        }
        int[] dp = new int[n];
        dp[0] = 1;
        dp[1] = 2;
        for (int i = 2 ; i < n; i++) {
            dp[i] = dp[i-1] + dp[i-2];
        }
        return dp[n-1];
    }
}

思路：动态规划

end