原题出处:https://leetcode.cn/leetbook/read/top-interview-questions-easy/xn8fsh/

解法一：

class Solution {
    public int maxProfit(int[] prices) {
        if (prices == null || prices.length == 0) {
            return 0;
        }
        int length = prices.length;
        // 没有持有股票时的最大值
        int nohold = 0;
        // 持有股票时的最大值
        int hold = -prices[0];
        for (int i = 1 ; i < length; i++) {
            nohold = Math.max(nohold,hold+prices[i]);
            hold = Math.max(hold,-prices[i]);
        }
        return nohold;
    }
}

思路：根据题目意思，股票只能在某一天中买入且只能买一次，股票也只能在某一天中卖出，也只能卖一次，我们期望的是卖出和买入的差值的最大的。

动态规划

• 确定状态
• 找到转移公式
• 确定初始条件以及边界条件
• 计算结果

定义两个变量，一个为持有股票时的最大值，一个为没有持有股票时的最大值，

初始化，持有股票时的最大利润为买入股票时的价格，这个时候利润为负数

没有持有股票时的最大利润为0；

遍历除第一天之后的每一天的股票数据，

没有持有股票时的最大值为当前的值与只有股票时的最大值和当前价格的和比较，较大的一个值为当前没有持有股票时的值

持有股票时的最大值为当前的值与当前价格的负数的一个比较大的一个值的结果。

遍历结束后，没有持有股票的利润最大值就是能够卖出的最大利润。

解法二：

class Solution {
    public int maxProfit(int[] prices) {
        if (prices == null || prices.length == 0) {
            return 0;
        }
        int min = prices[0];
        int max = 0;
        for (int i = 1 ; i < prices.length;i++) {
            min = Math.min(min,prices[i]);
            max = Math.max(max,prices[i]-min);
        }

        return max;
    }
}

思路：双指针，结果是找到股票能够获得的最大利润，那么我们只需要遍历数组将每次获取的最大利润进行计算再与当前利润进行比较，如果比当前利润大就进行替换即可，当然，在遍历的时候我们需要将当前的价格与当前的最小价格进行对比，如果较小，则进行替换。最后返回最大的利润即可。

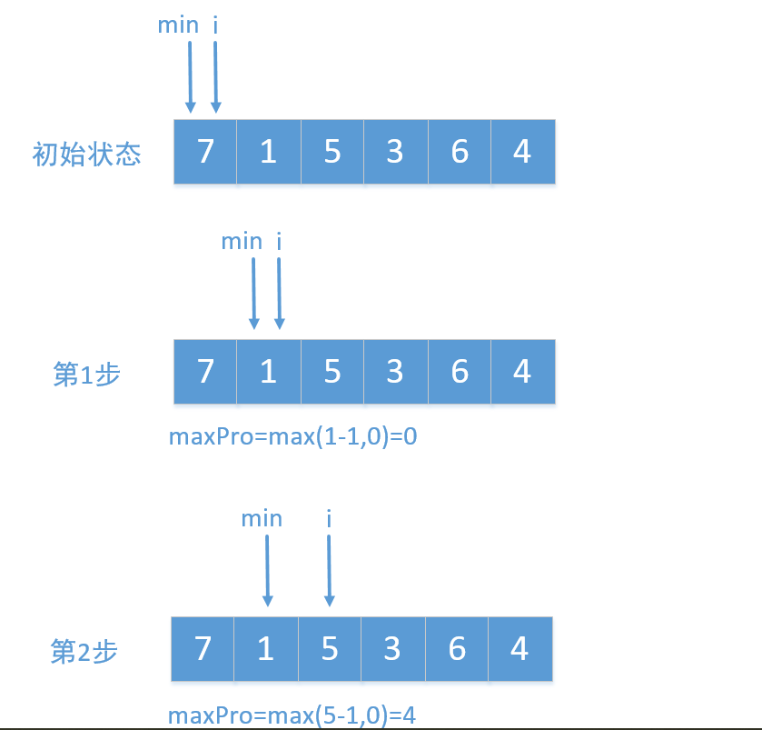
解法三：

class Solution {
    public int maxProfit(int[] prices) {
        if (prices == null || prices.length == 0) {
            return 0;
        }
        Stack<Integer> stack = new Stack();
        stack.push(prices[0]);
        int max = 0;
        for (int i = 1 ; i < prices.length; i++) {
            if (stack.peek() > prices[i]) {
                // 如果栈顶的元素大于当前价格，就将当前的价格替换到当前的栈顶元素
                stack.pop();
                stack.push(prices[i]);
            } else {
               // 如果栈顶的元素不大于当前的价格，就计算当前能够获取的最大利润
               max = Math.max(max,prices[i]-stack.peek());
            }
        }

        return max;
    }
}

思路：这个解法是也是一个双指针的特例，我们要始终保持栈顶元素是所访问过的元素中最小的。只不过是将最小价格的变量换成了一个栈来保存，计算当前价格是否小于当前栈顶价格，如果小于，那么将出栈，在压栈，将当前的价格入栈即可。

如果当前栈顶价格小于当前价格，那么就计算能够获取的利润，如果利润比当前的利润大那么就替换掉当前的最大利润。遍历结束后，将最大利润返回即可。