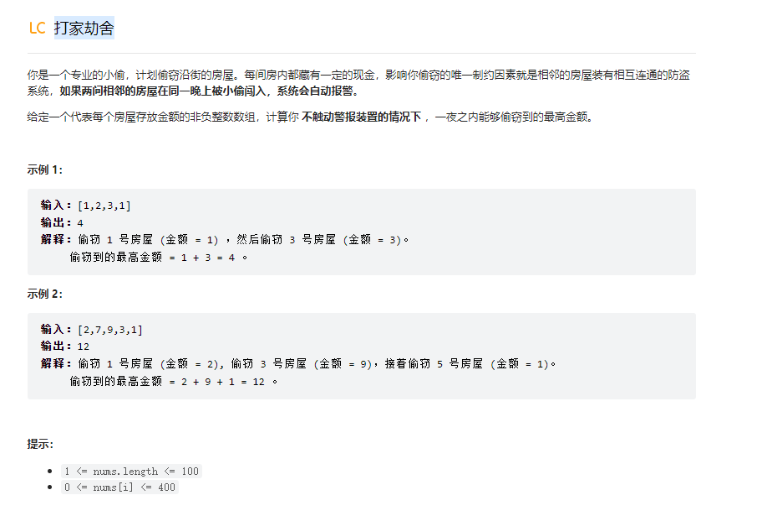
原题出处：https://leetcode.cn/leetbook/read/top-interview-questions-easy/xnq4km/

解法一：

class Solution {
    public int rob(int[] nums) {
        int length = nums.length;
        int dep0 = 0;
        int dep1 = nums[0];
        for (int i = 1 ; i < length; i++) {
            int tmp = Math.max(dep0,dep1);
            dep1 = dep0 + nums[i];
            dep0 = tmp;
        }
        return Math.max(dep0,dep1);
    }
}

思路：动态规划，

数组中的值表示的是存放的金额，小偷可以选择偷和不偷，如果前一个偷了，那么下一个肯定是不能偷的，因为相邻的房屋在同一晚上被小偷闯入，系统会自动报警。如果上一个没偷，那么下一个可以选择偷也可以选择不偷，视情况而定。

1，dp[i][0]=max(dp[i-1][0],dp[i-1][1])

他表示如果第i+1家没偷，那么第i家有没有偷都是可以的，我们取最大值即可。

2，dp[i][1]=dp[i-1][0]+nums[i]

他表示的是如果第i+1家偷了，那么第i家必须没偷，这里nums[i]表示的是第i+1家偷的金额。

递推公式找出来之后我们再来看下边界条件，第一家可以选择偷，也可以选择不偷，所以

dp[0][0]=0，第一家没偷

dp[0][1]=nums[0]，第一家偷了

解法二：

class Solution {
    public int rob(int[] nums) {
        return robHelper(nums,nums.length-1);
    }

    private int robHelper(int[] nums,int n) {
        // 终止条件
        if (n < 0) {
            return 0;
        }
        // 偷上上家能够获取的最大值
        int lastLast = robHelper(nums,n-2);
        // 偷上家能够获取的最大值
        int last = robHelper(nums,n-1);
        // 偷完上上家后还能再偷当前这家
        int cur = lastLast + nums[n];
        // 返回偷上家和当前这家的最大值即可
        return Math.max(last,cur);
    }

}

思路：递归，偷上上家，在偷上家，在把上上家和当前这家的加起来，比较谁更大，这个方法会超时，递归效率更低，因为有大量的重复计算。

参考文章：

动态规划解按摩师的最长预约时间