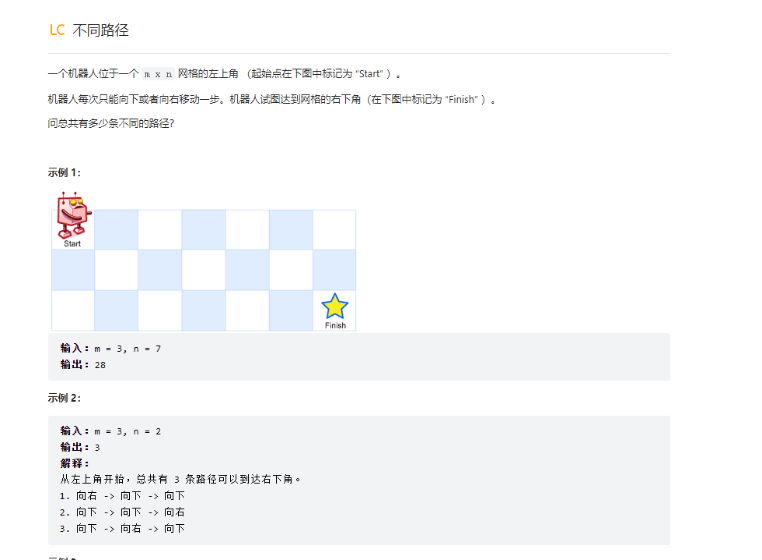
原题出处：https://leetcode.cn/leetbook/read/top-interview-questions-medium/xvjigd/

解法一：（python）

import math
class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        return int(math.factorial(m+n-2)/math.factorial(m-1)/math.factorial(n-1))

思路：根据题意我们知道机器人只能向下走或者向右走，那么它打到右下角，向下一定会走m-1步，向右一定会走n-1步，一共需要走m+n-2步，

那么我们就可以将这一过程转换为一个概率问题，从一共走的步数（m+n-2）中选取出（m-1）一共有多少中可能，即C(m+m-2,m-1)

2025-06-11 start:

解法二（java）:

class Solution {
    public int uniquePaths(int m, int n) {
        if (m == 1 || n == 1) {
            return 1;
        }
        int[][] dp = new int[m+1][n+1];
        for (int i = 1; i <= m; i++) {
            dp[i][1] = 1;
        }
        for (int i = 1; i <= n; i++) {
            dp[1][i] = 1;
        }
        for (int i = 2; i <= m ; i++) {
            for (int j = 2; j <= n; j++) {
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        return dp[m][n];
    }
}

思路：动态规划，要走到dp[m][n]就必须做到dp[m-1][n]或者dp[m][n-1]这里，所以dp[m][n] = dp[m-1][n] + dp[m][n-1],这里就是状态转移方程了，然后注意边界条件即可。

end