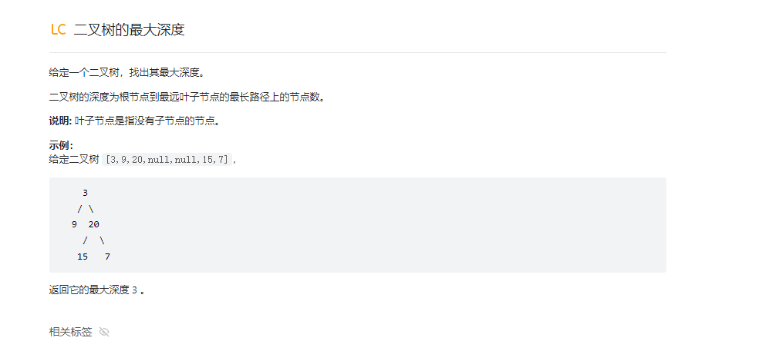
原题出处：https://leetcode.cn/leetbook/read/top-interview-questions-easy/xnd69e/

解法一：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        return Math.max(maxDepth(root.left),maxDepth(root.right))+1;

    }
}

思路：递归，获取左右子树最深的长度，将最长的返回即可。

解法二：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        Deque<TreeNode> deque = new LinkedList();
        deque.add(root);
        int count = 0;
        while(!deque.isEmpty()) {
            int size = deque.size();
            while(size-- > 0) {
                TreeNode treeNode = deque.pop();
                if (treeNode.left != null) {
                    deque.add(treeNode.left);
                }
                if (treeNode.right != null) {
                    deque.add(treeNode.right);
                }
            }
            count++;
        }
        return count;
    }
}

思路：广度优先搜索，就是遍历每一层并计数，最后返回每一层的数量即可。

解法三：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        Stack<TreeNode> stackNode = new Stack<>();
        Stack<Integer> stackCount = new Stack<>();
        stackNode.push(root);
        stackCount.push(1);
        int max = 0;
        while (!stackNode.isEmpty()) {
            TreeNode treeNode = stackNode.pop();
            int count = stackCount.pop();
            max = Math.max(count,max);
            if (treeNode.left != null) {
                stackNode.push(treeNode.left);
                stackCount.push(count+1);
            }
            if (treeNode.right != null) {
                stackNode.push(treeNode.right);
                stackCount.push(count+1);
            }
        }
        return max;
    }
}

思路：用两个栈，一个记录节点的stackNode 栈，一个记录节点所在层数的stackCount栈，stackNode 中每个节点在stackCount中都会有一个对应的值，并且他们是同时出栈，同时入栈