描述
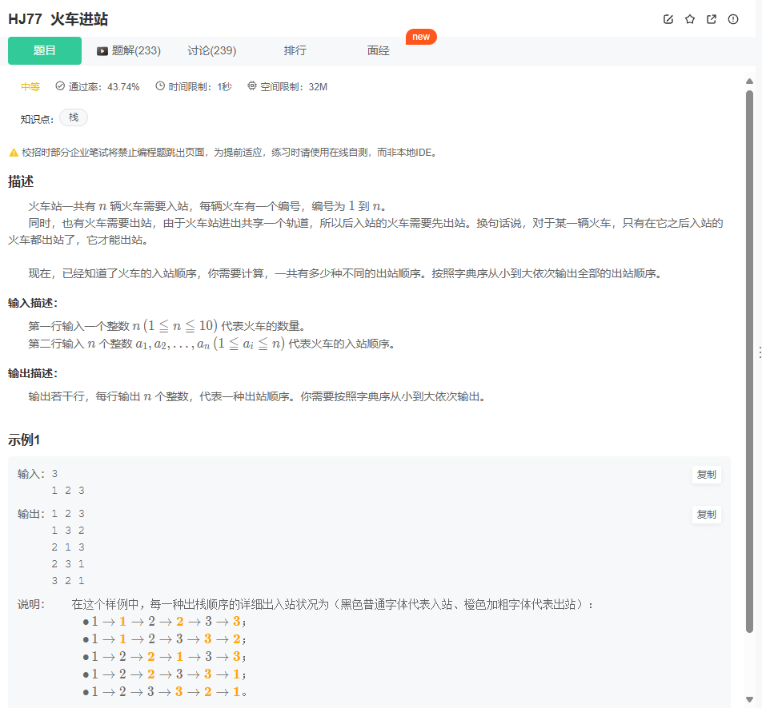
火车站一共有 n 辆火车需要入站,每辆火车有一个编号,编号为 1 到 n。
同时,也有火车需要出站,由于火车站进出共享一个轨道,所以后入站的火车需要先出站。换句话说,对于某一辆火车,只有在它之后入站的火车都出站了,它才能出站。
现在,已经知道了火车的入站顺序,你需要计算,一共有多少种不同的出站顺序。按照字典序从小到大依次输出全部的出站顺序。
同时,也有火车需要出站,由于火车站进出共享一个轨道,所以后入站的火车需要先出站。换句话说,对于某一辆火车,只有在它之后入站的火车都出站了,它才能出站。
现在,已经知道了火车的入站顺序,你需要计算,一共有多少种不同的出站顺序。按照字典序从小到大依次输出全部的出站顺序。
输入描述:
第一行输入一个整数 n(1≦n≦10) 代表火车的数量。
第二行输入 n 个整数 a1,a2,…,an(1≦ai≦n) 代表火车的入站顺序。
第二行输入 n 个整数 a1,a2,…,an(1≦ai≦n) 代表火车的入站顺序。
输出描述:
输出若干行,每行输出 n 个整数,代表一种出站顺序。你需要按照字典序从小到大依次输出。
解法一(java):
import java.util.*;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
// 注意 hasNext 和 hasNextLine 的区别
// while (in.hasNextInt()) { // 注意 while 处理多个 case
// int a = in.nextInt();
// int b = in.nextInt();
// System.out.println(a + b);
// }
int n = in.nextInt();
int[] array = new int[n];
for (int i = 0 ; i < n ; i++) {
array[i] = in.nextInt();
}
List<List<Integer>> tmpResult = new ArrayList<>();
backStarck(tmpResult, new ArrayList<>(), array);
List<List<Integer>> result = new ArrayList<>();
for (List<Integer> ls : tmpResult) {
if (isValid(ls, array)) {
result.add(ls);
}
}
result.sort((a1, a2)-> {
for (int i = 0; i < a1.size(); i++) {
if (a1.get(i) != a2.get(i)) {
return a1.get(i) - a2.get(i);
}
}
return 0;
});
for (List<Integer> ls : result) {
for (int i = 0 ; i < ls.size() ; i++) {
if (i == ls.size() - 1) {
System.out.print(ls.get(i));
} else {
System.out.print(ls.get(i) + " ");
}
}
System.out.println();
}
}
public static boolean isValid(List<Integer> outList, int[] inArray) {
Stack<Integer> stack = new Stack<>();
int index = 0;
for (int i = 0 ; i < inArray.length ; i++) {
int v = inArray[i];
stack.push(v);
while (!stack.isEmpty() && stack.peek().equals(outList.get(index))) {
stack.pop();
index++;
if (index == outList.size()) {
return stack.isEmpty();
}
}
}
return stack.isEmpty() && index == outList.size();
}
public static void backStarck(List<List<Integer>> tmpResult,
List<Integer> tmpList, int[] array) {
if (tmpList.size() == array.length) {
tmpResult.add(new ArrayList<>(tmpList));
return;
}
for (int i = 0 ; i < array.length ; i++) {
int v = array[i];
if (tmpList.contains(v)) {
continue;
}
tmpList.add(v);
backStarck(tmpResult, tmpList, array);
tmpList.remove(tmpList.size() - 1);
}
}
}思路:回溯法,首先我们使用全排列的思路获取所有的排列,然后在从所有的排列中过滤出满足要求的数据。