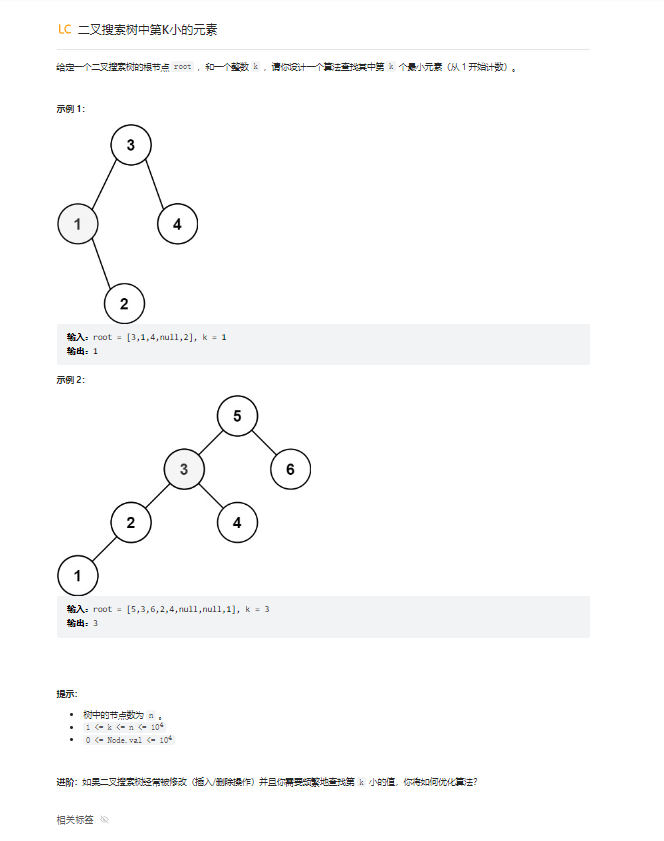
原题出处：https://leetcode.cn/leetbook/read/top-interview-questions-medium/xvuyv3/

解法一：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int count = 1;
    int target = -1;

    public int kthSmallest(TreeNode root, int k) {
        count = k;
        mid(root);
        return target;
    }

    public void mid(TreeNode node) {
        if (node == null) {
            return;
        }
        mid(node.left);
        if (--count == 0) {
            target = node.val;
        }
        mid(node.right);
    }
}

思路：

二叉查找树（英语：Binary Search Tree），也称为二叉查找树、有序二叉树（ordered binary tree）或排序二叉树（sorted binary tree），是指一棵空树或者具有下列性质的二叉树：

若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值；

若任意节点的右子树不空，则右子树上所有节点的值均大于它的根节点的值；

任意节点的左、右子树也分别为二叉查找树；

根据上面的性质，我们就能够知道，我们通过一个中序遍历，就能够得到一个有序的数组，然后我们根据k的值拿到对应数组值即可。

中序遍历：

public void mid(TreeNode root) {
       if (root == null) {
           return;
       }
       mid(root.left);
      System.out.println(root.value);
      mid(root.right);
}

解法二：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {

    public int kthSmallest(TreeNode root, int k) {
        int size = count(root.left);
        if (size >= k) {
            return kthSmallest(root.left,k);
        } else if (size + 1 == k) {
            return root.val;
        } else {
            return kthSmallest(root.right,k-1-size);
        }
    }

    public int count(TreeNode node) {
        if (node == null) {
            return 0;
        }
        return 1 + count(node.left) + count(node.right);
    }
}

思路：我可以先统计出从根节点出发的左子树数量，如果数目大于或等于k的值，那么就继续递归左子树，数目+1等于k的值，那么就表示，当前的值就是我们要找的值，否则，我们就遍历右子树，注意在遍历右子树的时候k的值要减去1和左子树的数量。