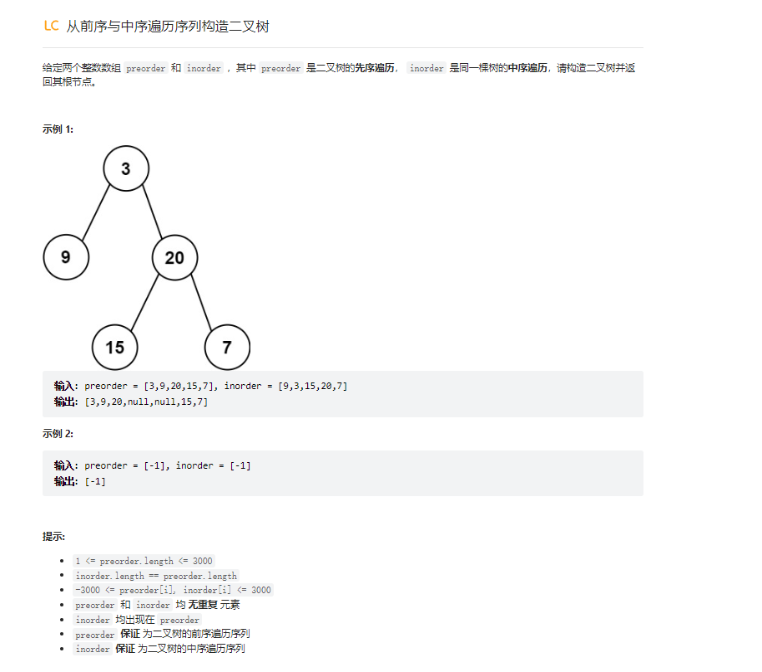
原题出处：https://leetcode.cn/leetbook/read/top-interview-questions-medium/xvix0d/

解法一：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        List<Integer> preList = new ArrayList<>();
        List<Integer> inList = new ArrayList<>();
        for (int i = 0 ; i < inorder.length; i++) {
            preList.add(preorder[i]);
            inList.add(inorder[i]);
        }
        return helper(preList,inList);
    }

    public TreeNode helper(List<Integer> preList,List inList) {
        if (inList.size() == 0) {
            return null;
        }
        Integer rootVal = preList.remove(0);
        TreeNode root = new TreeNode(rootVal);
        int mid = inList.indexOf(rootVal);
        root.left = helper(preList,inList.subList(0,mid));
        root.right = helper(preList,inList.subList(mid+1,inList.size()));
        return root;
    }
}

思路：递归的方式进行构建，我们先将数组转化为一个集合，因为集合好操作一点，每次取出前序集合中的第一个元素，这是二叉树的根，然后构造一个根节点，在递归左子树和右子树，左子树的中序集合就是上一个中序集合的根数值的左边部分即inList.subList(0,mid)，右子树的中序集合就是上一个中序集合的根数值的右边部分即inList.subList(mid+1,inList.size())，然后返回根节点即可。